Las funciones cóncavas y convexas son conceptos fundamentales en el estudio del cálculo y la optimización. Estas funciones, presentes en diversos campos como la economía, la física y la ingeniería, tienen propiedades particulares que las hacen especialmente interesantes. En este artículo, exploraremos en profundidad las características y aplicaciones de las funciones cóncavas y convexas, así como su importancia en la resolución de problemas reales. Acompáñanos en este fascinante recorrido por el mundo de las funciones y descubre cómo pueden ayudarnos a encontrar soluciones eficientes y óptimas.
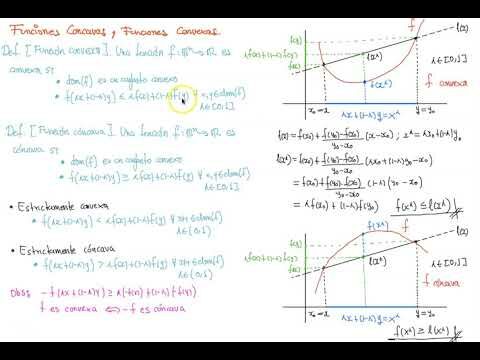
- Las funciones cóncavas presentan una curva hacia abajo, mientras que las funciones convexas presentan una curva hacia arriba.
- En una función cóncava, el cociente incremental de las diferencias entre los puntos de la función es siempre decreciente.
- En una función convexa, el cociente incremental de las diferencias entre los puntos de la función es siempre creciente.
- Las funciones cóncavas alcanzan su valor mínimo en el punto de inflexión de la curva, mientras que las funciones convexas alcanzan su valor máximo en dicho punto.
- Las funciones cóncavas y convexas son ampliamente utilizadas en economía, matemáticas y ciencias naturales para modelar fenómenos que presentan comportamientos de crecimiento y decrecimiento.
¿Qué diferencia hay entre cóncavo y convexo?
La diferencia entre cóncavo y convexo radica en la forma en que los objetos se curvan. Un objeto es cóncavo cuando parece tener una concavidad o una curva hacia adentro, como un cuenco vacío que se hunde hacia el centro. Por otro lado, un objeto es convexo cuando parece tener una convexidad o una curva hacia afuera, como una esfera que sobresale hacia el exterior. Estas diferencias en la forma de curvatura hacen que los objetos cóncavos parezcan más profundos, mientras que los objetos convexos parecen más salientes.
¿Bajo qué condiciones una función es cóncava?
Una función es cóncava cuando el segmento que une dos puntos cualesquiera queda por debajo de la curva, lo que indica que su concavidad está hacia abajo. Esto significa que la curva de la función es curvada hacia abajo en lugar de hacia arriba, lo que se puede observar visualmente.
¿Cuál es el criterio para determinar si una función es convexa?
Una forma de determinar si una función es convexa es verificando si la cuerda que une dos puntos cualesquiera en el grafo de la función se encuentra siempre por encima de la función. Si esto se cumple en un intervalo específico (a, b), entonces podemos afirmar que la función es convexa en ese intervalo.
La convexidad de una función se puede visualizar mediante el análisis de su gráfica. Si al trazar una cuerda entre dos puntos en el gráfico, esta se mantiene siempre por encima de la función, entonces podemos concluir que la función es convexa. Este criterio es útil para determinar la convexidad de una función en un intervalo determinado.
En resumen, para saber si una función es convexa, debemos verificar si la cuerda que une cualquier par de puntos en el gráfico de la función se encuentra siempre por encima de la función. Este criterio nos permite determinar la convexidad de una función en un intervalo específico (a, b).
Maximiza tu eficiencia: Aprende a optimizar funciones cóncavas y convexas
En el mundo acelerado de hoy, maximizar nuestra eficiencia es fundamental para lograr el éxito. Afortunadamente, aprender a optimizar funciones cóncavas y convexas puede ser la clave para alcanzar este objetivo. Las funciones cóncavas son aquellas en las que el gráfico se curva hacia abajo, mientras que las funciones convexas se curvan hacia arriba. Al dominar estas técnicas matemáticas, podrás tomar decisiones más inteligentes y eficientes en tu vida personal y profesional.
La optimización de funciones cóncavas y convexas puede tener un impacto significativo en tu productividad. Por ejemplo, al analizar una función cóncava, podrás identificar rápidamente el punto máximo y, por lo tanto, el mejor resultado posible. Esto te permitirá enfocar tus esfuerzos y recursos en las áreas más rentables y eficientes. Por otro lado, al optimizar una función convexa, podrás encontrar el punto mínimo, lo que te ayudará a reducir costos y maximizar tus ganancias.
Además de sus beneficios económicos, aprender a optimizar funciones cóncavas y convexas también te ayudará a tomar decisiones más informadas en tu vida diaria. Por ejemplo, al aplicar estas técnicas a problemas de planificación de tiempo, podrás identificar cuándo y cómo realizar ciertas tareas para maximizar tu productividad. También podrás utilizar estas habilidades para analizar opciones de inversión y seleccionar la estrategia más rentable. En resumen, dominar la optimización de funciones cóncavas y convexas te brindará las herramientas necesarias para maximizar tu eficiencia en todos los aspectos de tu vida.
La clave de la simplicidad: Cómo alcanzar la concisión en funciones cóncavas y convexas
La simplicidad es una habilidad clave en matemáticas y, en particular, en el estudio de funciones cóncavas y convexas. Estas funciones son fundamentales en el análisis de optimización y ofrecen soluciones eficientes y elegantes a diversos problemas. Para alcanzar la concisión en estas funciones, es fundamental comprender la estructura de las mismas y utilizar técnicas adecuadas de simplificación. Al eliminar redundancias y términos innecesarios, se logra una mayor claridad y facilidad de comprensión, lo que permite una representación más concisa y atractiva de estas funciones.
Al simplificar funciones cóncavas y convexas, se logra resaltar su belleza intrínseca y su poder para resolver problemas complejos de manera eficiente. La clave para alcanzar la concisión en estas funciones radica en identificar los elementos esenciales y eliminar toda información redundante o superflua. Esto no solo facilita su comprensión, sino que también permite su aplicación en diferentes contextos y situaciones. En resumen, la simplicidad y la concisión son fundamentales para aprovechar al máximo el potencial de las funciones cóncavas y convexas, brindando soluciones efectivas y elegantes a los desafíos matemáticos.
En resumen, las funciones cóncavas y convexas son herramientas fundamentales en el análisis matemático que nos permiten comprender y modelar una amplia gama de fenómenos en diversos campos. Su comportamiento distintivo y sus propiedades bien definidas nos brindan una base sólida para el estudio y la resolución de problemas complejos. Ya sea en economía, física, ingeniería u otras disciplinas, el entendimiento de estas funciones nos proporciona una valiosa perspectiva para tomar decisiones informadas y alcanzar soluciones óptimas.